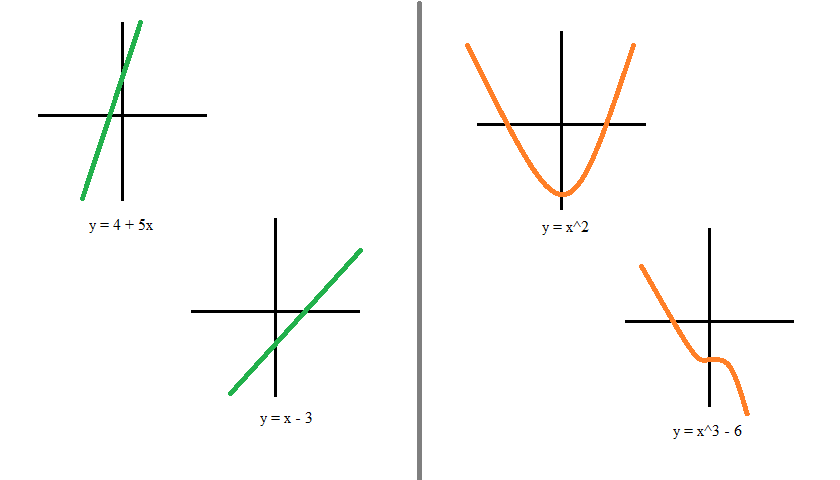When you are solving maths questions, you’ve probably encountered different kinds of equations. A few Equations are composed of only numbers. Others consist of only variables, and some comprise variables and numbers.
Equations that are nonlinear or linear generally comprise variables and numbers. Before we get into the differences between non-linear and linear equations, we must first know the meaning of Linear and Non-Linear equations.
Linear Equation:
A linear equation forms a straight line. Linear refers to anything related to the line. The linear equations can be utilised to create lines. Linear Equations are the conditions of the primary demand, and lines define them within the arranged framework.
Linear equations are equations that have just one solution: the straight line. Straight-line conditions may be expressed as y=mx+b, where m is the slope of the line, and the slant is m of the line, and B is they-catch.
Non-Linear Equations:
Non-linear equations are not straight lines. It appears as the shape of a curve on the graph and has a variable slope.
The non-linear equation is typically expressed as the equation ax 2.+by 2. = c
where the variables x and y are
A, B, and C are constant values.
The most significant distinction between nonlinear and linear equations is explained here to help students to be able to grasp the concept more naturally. The differences are presented in tabular form, accompanied by examples.
What is the main difference between Linear as well as Nonlinear Equations?
To understand the difference between these two equations, i.e. nonlinear and linear, one must know the definitions of these equations.
Let us first determine and discover the linear and nonlinear equations differences:
| Linear Equations | Non-Linear Equations |
| It creates a uniform line, or it represents the equation of the straight line | It doesn’t form consecutive lines but instead makes the shape of a curve. |
| It is a single degree. It is also possible to consider it an equation with the highest degree of 1. | A nonlinear equation has a degree of 2 or greater than 2; however, it is not less than. |
| Each of these equations forms straight lines in the XY plane. It can extend these lines in any direction, but they must be in a straight line. | It creates a curve. When we increase the degree that we increase the degree, the curvature on the graph will increase. |
| The most common representation of a linear equation is-
y = mx +c The variables x and two variables. m represents the slope, and C is a constant. |
The general representation for nonlinear equations is-
ax 2 + by 2 = c The variables x and the variables and a,b , and c are the constant values. |
Examples:
|
Examples:
|
Note:
The linear equation is composed of only one variable, and If an equation has two variables, the equation can be classified as one Linear equation with two variables. For instance, 5x + 2 = 1 can be described as a linear equation in one variable. However, 5x + 2y =1 can be described as one Linear equation with two variables.
Let’s take a look at some examples that are based on these ideas.
Solved Examples
Example: Solve the linear equation 3x+9 = 2x +18.
Solution: Given, 3x+9 = 2x + 18
= 3x – 2x = 18 – 9
= x = 9
Examples: Solve the nonlinear equation x+2y = 1, and it is x x.
Solution: Given, x+2y = 1
x = y =
In the event that we place an x value into the first equation, we will receive,
= y + 2y = 1
= 3y = 1
= y = 1/3
x = y = 1/3
Example: Solve x = 12(x +2)
Solution:
* = 12(x + 2)
*x=12x+24
Subtract 24 from each of the sides.
12x = x + 24 + 24
12x = x 24 = 12x
Simplify
11x = -24
Separate x by splitting each side by 11.
11x / 11 = -24/11
x = 24/11
Example: Solution to the nonlinear equation x+4y = 1. and the equation x = y.
Solution:
Given, x+4y = 1
x = y =
In the event that we place an x value into the first equation, we will receive,
= y + 4y = 1
= 4y = 1
= y = 1/4
x = y = 1/4
Example: Solve the equation that is nonlinear, x + 2y =1 and the equation x = 2
Solution:
Given, x+2y = 1
2.x =
When we put an x value into the first equation, we will find,
= 2+ 2y = 1
= 2y = -1
= y = -1/2
y=½
Example: Solve the Linear problem 9(x + 1) = 2(3x + 8)
Solution:
9(x + 1) = 2(3x + 8)
Expand each side
9x + 9 = 6x + 16
Subtract 6x from both sides
9x + 9 – 6x = 6x + 16 – 6x
3x + 9 = 16
Subtract 9 from both sides
3x + 9 – 9 = 16 – 9
3x = 7
Divide each one by 3
3x/3 = 7/3
x = 7/3
Example: Solve the nonlinear equation
3×2 – 5x + 2 = 0
Solution:
3×2 – 5x + 2 = 0
Factorising
3×2 – 3x – 2x + 2 = 0
3x(x – 1) – 2(x – 1) = 0
( 3x – 2)( x – 1) = 0
(3x – 2) = 0 or (x – 1) = 0
2/3 of x = 1
Quiz Time
- Solve the linear equation below and determine the value of the variable x
- 3(5x + 6) = 3x – 2
- (2x +9)/5 = 5
- Find the equations that are nonlinear.
- 7×2 = 8 – 10x
- 3(x2 – 4) = 5x
What is the primary difference between linear and nonlinear equations?
The linear equation can be utilised to represent straight lines in a graph. In contrast, non-linear equations can be used to depict curves.
What graph of non-linear and linear equations appears?
A linear equation graph has an equation with a constant slope, whereas the graphs of non-linear equations reveal the slope variations at various places.
How can the linear equation be expressed? Illustrate.
The most common definition of linear equations is: y = MX + c where m = the slope of the line
Two variables, x, and variables
C is the interception (constant value)
Example: 2x+y=1
y=-2x+1
How do you get the nonlinear equation to be constructed?
A non-linear equation can be described by an x 2 +by 2 = c
where the variables x and y are A, B and C are all constant values.
Conclusion
To determine the differences between these two equations, i.e. linear and nonlinear, you should be aware of the definitions for these equations. Let us first identify and examine the differences between the two.